Find a cycle in a directed graph in Java

Recently I had to solve a problem that involving detecting cycle in a directed graph. I did some googling to see what other people have done. There are some good ideas on the web but nothing was exactly the right approach I’d like. So I wrote my own algorithm and Java implementation.

Directed Graph and DAG

In mathematics, a graph is a structure that consists of a group of nodes and the lines that connect these nodes. Each node is called a vertex and the lines that connect the nodes are called edges. A directed graph is a graph in which the edges have direction; they point from one vertex to another or from a vertex to itself. A real life example of a directed graph is a flow chart.

A directed graph can contain cycles. A cycle exists if we can, starting from a particular vertex, follow the edges in the forward direction and eventually loop back to that vertex. A graph that has no directed cycle is an directed acyclic graph (DAG).

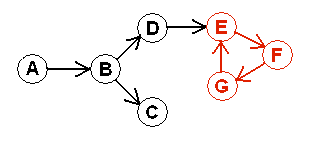
 Fig.1 A directed graph containing a cycle

When coding a directed graph you should consider different ways of implementing it depending on how connected your data is and what types of algorithms you’ll be using. We’ll show one way below, then we’ll implement a hasCycle() method which is based on a breadth-first topological sorting algorithm.

Implement Graph in Java

The implementation our graph will need a Graph class and two other classes, Vertex and Edge. We could have had only edges, each with a source and destination property, and let the vertices be implied but then we could not represent disconnected vertices. So let’s first look at how the Edge class is implemented.

public class Edge {

   public Vertex destination; // The destination Vertex of the Edge

   public Edge( Vertex d ){

      destination = d;

   }

}

Notice Edge stores a reference to the destination Vertex but not the source Vertex. That’s because in the Vertex class, we’ll store a list of the outbound Edges. This means that algorithms that need to traverse our graph can efficiently go from a Vertex to one of its outbound Edges, then to that Edge’s destination Vertex and so forth.

public class Vertex {

   public String name;

   public List<Edge> outEdges; // The out-bound Edges of this Vertex

   public int inDegree; // A convenient *scratch variable* for our algorithm to use

   public Vertex( String nm ){

      name = nm;

      outEdges = new LinkedList<Edge>();

      InDegree = 0;

   }

}

Now we can write an interface for our graph.

interface Graph {

   public Set<Vertex> vertices(); // Return all Vertices in the Graph

   public addVertex( String name );

   public void addEdge( String sourceName, String destName );

   public long size(); // Return the number of Vertices in the Graph

}

An implementation of Graph would store a collection of Vertices. The collection could be a Map with key of Vertex name for instance.

Implement the Search Method

Let’s look at an algorithm which will determine if our graph contains a cycle. There are different approaches to this problem – we’ll look at another way in a future post. In this method we use the idea that a directed graph whose vertices each have at least one incoming edge is itself a cycle. So our search will continue to remove vertices and their out-bound edges until what remains meets that condition. If we traverse the whole graph without seeing that condition then there is no cycle.

public static boolean hasCycle(DirectedGraph graph){

   if (graph == null || graph.size() == 0) return false;

   Collection <Vertex>vertexCollect = graph.vertices();

   Queue <Vertex> q; // Queue will store vertices that have in-degree of zero

   long counter = 0;

   /* Calculate the in-degree of all vertices and store on the Vertex */

   for (Vertex v: vertexCollect)

      v.inDegree = 0;

   for (Vertex v: vertexCollect){

      for(Edge edge : v.outEdges())

         edge.dest().inDegree++;

      }

   /* Find all vertices with in-degree == 0 and put in queue */

   q = new LinkedList<Vertex>();

   for (Vertex v : vertexCollect){

      if (v.inDegree == 0)

         q.offer(v);

   }

   if(q.size() == 0){

   return true; // Cycle found – all vertices have in-bound edges

   /* Traverse the queue counting Vertices visited */

   for (counter = 0; !q.isEmpty(); counter++) {

      Vertex v=q.poll();

      for (Edge e: v.outEdges()){

         Vertex w = e.dest();

         if(–w.inDegree == 0){

            q.offer(w);

         }

      }

   }

   if (counter != vertexCollect.size() ){

      return true;  //Cycle found

   }

   return false;

}

Summary

So we start by calculating the starting inDegree for each Vertex. Each Vertex with inDegree == 0 is put into a queue. These Vertices are starting points for processing. We begin the search from a Vertex in the queue, following the Edges and keeping a count of the Vertices visited. We decrement the inDegree of Vertices as their in-bound Edges are processed. Vertices whose inDegree goes to zero are put into the queue. When we reach the end of a branch where there are no more out-bound Edges, we take another Vertex from the queue and traverse. If we empty the queue before we’ve visited all the Vertices then we’ve found a cycle.

Our algorithm is essentially a modified topological sort. It is based on a breadth-first search (BFS) stategy – all sibling outEdges of a Vertex are processed before moving down to the next layer of Vertices. It has a linear running time of O (|V| + |E|). In the worst case scenario there would be no cycle in the graph and we’d visit each Vertex and each Edge.

There are other approaches. Instead of using a BFS, we could use DFS (depth-first search). A typical DFS would be written with a recursive method. To find a cycle, instead of tracking inDegree and number of vertices visited, it would be looking for the condition of visiting a vertex twice in the same branch.

In a future post, Floyd’s Algorithm – Tortoise and Hare, we explore an alternate approach to finding cycles.