Posts Tagged ‘data structures’
When Recursion Goes Wrong
When I was in college, my text book used a Fibonacci example to explain how recursion worked. Later on the job I needed to write a program in recursion. After the program ran eight to nine hours, my machine ran out of memory. It was a case of recursion went wrong. In fact, it can go very wrong sometimes. What I was taught in school to use recursion to solve Fibonacci problem is a classic example of bad recursion.
Bad recursion can increase runtime in an exponential number
Recursion can be very powerful is by using its ‘divide and conquer’ strategy. A recursion with good algorithm can cut the run time to a fraction of the time when only use for loops.
But since recursion breaks the problem into sub problems, the number of sub problems can increase in an exponential number, thus make runtime to increase explosively. How can this happen? Let’s look at Fibonacci in recursion.
Fibonacci function:
1. fib(0)=1
2. fib(1)=1
3. fib(n)=fib(n-1) + fib(n-2) (n>=2)
The recursive implementation of Fibonacci function:
int fib( int n) {
if( n <= 1)
return 1;
else
return fib(n – 1) + fib(n – 2);
}
This is a classic example of recursion going horrible wrong. If we look carefully, it does repetitive work of recursive calling without using the sum from sub problem.
N=2, fib(2) = fib (1)+ fib(0) 2 calls to compute fib(1) and fib(0)
N=3, fib(3) = fib(2) + fib(1) 2 separate calls to compute fib(2) and fib(1), in which fib(2) = fib(1) + fib(0) . fib(1) is called 2 times. fib(0) 1 time.
N=4, fib(4) = fib(3) + fib(2).
Separate calls to compute fib(3) and fib(2). fib(3) =fib(2)+fib(1).
fib(3) is called 1 time, fib(2) is called2 times, fib(1)
is called 3 times and fib(0) is called 2 times.
N=5, fib(5) = fib(4) + fib(3), fib(4) is called once, fib(3) is called twice, fib(2) is called 3 times, fib(1) is called 5 times, fib(0) is called 3 times.
……
N=n, f(n) = f(n-1) + f(n-2), f(n-1) is called 1 time, f(n-2) is called 2 times, f(n-3) is called 3 times, f(n-4) is called 5 times.
How to fix the problem
The problem of the explosive calls in this recursion method is caused by recursive method spawns separate calls without reusing the computing results from the subproblem. To calculate fib(n) = fib (n-1) + fib(n-2), we can calculate from the base condition and use the sum when we go forward:
fib(0)=1;
fib(1)=1;
fib(2) = f(1) + f(0) = 1+1= 2;
fib(3)= f(2) +f(1) = 2+1= 3;
fib(4)= f(3) +f(2) = 3+2= 5;
……
int fib( int n ){
//base condition f(0)=1, f(1)=1
fibPrev =1;
fibNext=1;
if(n<2){
return 1;
}
/*if n>=2, we will compute the sub problem first and
use the sum for further computation*/
for(int i =2;i<=n;i ++)
{
fibSum = fibNext+fibPre ;
fibPre = fibNext ;
fibNext = fibSum;
}
return fibSum ;
}
So the above implementation illustrates that the problem can be solved by using for loop instead of using recursion. The for loop is a constant running time with O(n), compared to what is an exponential growth in recursion
scenario.
Summary
Sometimes a problem seems to be a perfect fit for recursion can actually be solved by a simple for loop solution with better performance. When the result from the sub problem is not used efficiently by the recursion call stack and computation is done redundantly, the running time can grow explosively. This is when the recursion can go horribly wrong.
Floyd’s Algorithm – Tortoise and Hare
Methodology
In a recent post we talked about finding a cycle in a graph using a breadth first search (BFS) and modified topological sort approach. Here we’ll look at another method, Floyd’s cycle finding algorithm, nicknamed The Tortoise and the Hare, which detects a cycle differently from our previous method. In the prevous post the idea is to eliminate all vertices and edges that are not part of cycles so that what’s left is a cycle or cycles. Floyd’s algorithm finds cycles directly – it recognizes that it’s traversing a cycle. This has the advantage of allowing us to get the cycle length. Previously we could have easily totaled the vertices remaining in the cycles but since we never traversed the cycles we didn’t know how many cycles there were or their lengths.
Another characteristic of Floyd’s algorithm is that it is well suited for space complexity since it stores only two pointers that move through the graph. One pointer, the hare, moves twice as fast as the other, the tortoise, and if the two meet we know they’re in a cycle. To simplify the example we’ll start with a functional graph. In a functional graph the vertices can have no more than one outbound edge. So each vertex can be thought of as having a function (edge) that returns the next vertex, or null if there’s no outbound edge.

Fig.1 A functional graph containing a cycle
In the code, instead of a Vertex.outEdges() method as before, we have outEdge() which returns a single Edge containing the destination Vertex. Here’s a Java implementation that begins at a passed-in start Vertex and makes the tortoise and hare race through the graph.
Floyd’s Algorithm
Note that to further simplify things we have considered searching only one branch of the graph. In the previous post we handled multiple incoming edges by having our iteration loop exist inside of an enclosing loop that made sure we tried all branches. Here we’re seeing only the inner loop that begins at the given start vertex and traverses until it hits a dead-end or a cycle. The hare takes 2 steps for each single tortoise step so they will land together on the same vertex only if they’re in a cycle. Using the example in Figure 1, and looking at the index numbers of the vertices, the steps progress like this:
| Tortoise | 0 | Hare | 0 | Starting line | |||||
| Tortoise | 1 | Hare | 2 | ||||||
| Tortoise | 2 | Hare | 4 | ||||||
| Tortoise | 3 | Hare | 6 | ||||||
| Tortoise | 4 | Hare | 8 | ||||||
| Tortoise | 5 | Hare | 10 | ||||||
| Tortoise | 6 | Hare | 12 | 6 and 12 are the same vertex – “G” |
The tortoise has moved ahead 6 vertices and the hare has moved 12 and they met on the “G” vertex so we know there’s a cycle. Now we may want to get some other values too like the length of the sequence before the cycle (the tail length), and the length of the cycle itself.
Tail Length
We can get the tail length by starting one pointer at the beginning and starting the tortoise where we left it and having each advance one step at a time until they meet. They will always meet at the vertex where the tail ends and the cycle begins.
| Tail Pointer | 0 | Tortoise | 6 | Starting line | |||||
| Tail Pointer | 1 | Tortoise | 7 | ||||||
| Tail Pointer | 2 | Tortoise | 8 | ||||||
| Tail Pointer | 3 | Tortoise | 9 | ||||||
| Tail Pointer | 4 | Tortoise | 10 | Same vertex – “E” |
Now we know “E” is the start of the cycle and if we’ve kept count we know that the tail is 4 edges long.
Cycle Length
To calculate the cycle length we can get the total graph length from vertex zero, around the cycle once and then subtract the tail length. When we ran the “tail length” step above, the tortoise ended up at the cycle start vertex but its index doesn’t give us the correct total graph length because it may have been around the loop more than once. So first start the tortoise back where it met the hare at vertex “G” (index 6) and advance until we reach the cycle start while noting the count. The tortoise begins on index 6, moves ahead one to “E” for a total graph length of 7 steps. Then we just subtract the tail length of 4 which gives us the cycle length, 3.
Complete Implementation
Test
A test that passes in the Vertices from Figure 1, and Vertex “A” as the starting point will print the following results:
Cycle found
Tail length is: 4
Cycle start Vertex is: E
Cycle length is: 3
Find a cycle in a directed graph in Java
Recently I had to solve a problem that involving detecting cycle in a directed graph. I did some googling to see what other people have done. There are some good ideas on the web but nothing was exactly the right approach I’d like. So I wrote my own algorithm and Java implementation.
Directed Graph and DAG
In mathematics, a graph is a structure that consists of a group of nodes and the lines that connect these nodes. Each node is called a vertex and the lines that connect the nodes are called edges. A directed graph is a graph in which the edges have direction; they point from one vertex to another or from a vertex to itself. A real life example of a directed graph is a flow chart.
A directed graph can contain cycles. A cycle exists if we can, starting from a particular vertex, follow the edges in the forward direction and eventually loop back to that vertex. A graph that has no directed cycle is an directed acyclic graph (DAG).
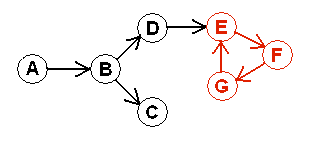
Fig.1 A directed graph containing a cycle
When coding a directed graph you should consider different ways of implementing it depending on how connected your data is and what types of algorithms you’ll be using. We’ll show one way below, then we’ll implement a hasCycle() method which is based on a breadth-first topological sorting algorithm.
Implement Graph in Java
The implementation our graph will need a Graph class and two other classes, Vertex and Edge. We could have had only edges, each with a source and destination property, and let the vertices be implied but then we could not represent disconnected vertices. So let’s first look at how the Edge class is implemented.
Notice Edge stores a reference to the destination Vertex but not the source Vertex. That’s because in the Vertex class, we’ll store a list of the outbound Edges. This means that algorithms that need to traverse our graph can efficiently go from a Vertex to one of its outbound Edges, then to that Edge’s destination Vertex and so forth.
Now we can write an interface for our graph.
An implementation of Graph would store a collection of Vertices. The collection could be a Map with key of Vertex name for instance.
Implement the Search Method
Let’s look at an algorithm which will determine if our graph contains a cycle. There are different approaches to this problem – we’ll look at another way in a future post. In this method we use the idea that a directed graph whose vertices each have at least one incoming edge is itself a cycle. So our search will continue to remove vertices and their out-bound edges until what remains meets that condition. If we traverse the whole graph without seeing that condition then there is no cycle.
Summary
So we start by calculating the starting inDegree for each Vertex. Each Vertex with inDegree == 0 is put into a queue. These Vertices are starting points for processing. We begin the search from a Vertex in the queue, following the Edges and keeping a count of the Vertices visited. We decrement the inDegree of Vertices as their in-bound Edges are processed. Vertices whose inDegree goes to zero are put into the queue. When we reach the end of a branch where there are no more out-bound Edges, we take another Vertex from the queue and traverse. If we empty the queue before we’ve visited all the Vertices then we’ve found a cycle.
Our algorithm is essentially a modified topological sort. It is based on a breadth-first search (BFS) stategy – all sibling outEdges of a Vertex are processed before moving down to the next layer of Vertices. It has a linear running time of O (|V| + |E|). In the worst case scenario there would be no cycle in the graph and we’d visit each Vertex and each Edge.
There are other approaches. Instead of using a BFS, we could use DFS (depth-first search). A typical DFS would be written with a recursive method. To find a cycle, instead of tracking inDegree and number of vertices visited, it would be looking for the condition of visiting a vertex twice in the same branch.
In a future post, Floyd’s Algorithm – Tortoise and Hare, we explore an alternate approach to finding cycles.