When Recursion Goes Wrong

When I was in college, my text book used a Fibonacci example to explain how recursion worked. Later on the job I needed to write a program in recursion. After the program ran eight to nine hours, my machine ran out of memory. It was a case of recursion went wrong. In fact, it can go very wrong sometimes. What I was taught in school to use recursion to solve Fibonacci problem is a classic example of bad recursion.

Bad recursion can increase runtime in an exponential number

Recursion can be very powerful is by using its ‘divide and conquer’ strategy. A recursion with good algorithm can cut the run time to a fraction of the time when only use for loops.

But since recursion breaks the problem into sub problems, the number of sub problems can increase in an exponential number, thus make runtime to increase explosively. How can this happen? Let’s look at Fibonacci in recursion.

Fibonacci function:

1. fib(0)=1
2. fib(1)=1
3. fib(n)=fib(n-1) + fib(n-2) (n>=2)

The recursive implementation of Fibonacci function:

int fib( int n) {
if( n <= 1)
return 1;
else
return fib(n – 1) + fib(n – 2);
}

This is a classic example of recursion going horrible wrong. If we look carefully, it does repetitive work of recursive calling without using the sum from sub problem.

N=2, fib(2) = fib (1)+ fib(0) 2 calls to compute fib(1) and fib(0)

N=3, fib(3) = fib(2) + fib(1) 2 separate calls to compute fib(2) and fib(1), in which fib(2) = fib(1) + fib(0) . fib(1) is called 2 times. fib(0) 1 time.

N=4, fib(4) = fib(3) + fib(2).
Separate calls to compute fib(3) and fib(2). fib(3) =fib(2)+fib(1).
fib(3) is called 1 time, fib(2) is called2 times, fib(1)
is called 3 times and fib(0) is called 2 times.

N=5, fib(5) = fib(4) + fib(3), fib(4) is called once, fib(3) is called twice, fib(2) is called 3 times, fib(1) is called 5 times, fib(0) is called 3 times.

……

N=n, f(n) = f(n-1) + f(n-2), f(n-1) is called 1 time, f(n-2) is called 2 times, f(n-3) is called 3 times, f(n-4) is called 5 times.

How to fix the problem

The problem of the explosive calls in this recursion method is caused by recursive method spawns separate calls without reusing the computing results from the subproblem. To calculate fib(n) = fib (n-1) + fib(n-2), we can calculate from the base condition and use the sum when we go forward:

fib(0)=1;
fib(1)=1;
fib(2) = f(1) + f(0) = 1+1= 2;
fib(3)= f(2) +f(1) = 2+1= 3;
fib(4)= f(3) +f(2) = 3+2= 5;
……

int fib( int n ){
//base condition f(0)=1, f(1)=1
fibPrev =1;
fibNext=1;
if(n<2){
return 1;
}
/*if n>=2, we will compute the sub problem first and
use the sum for further computation*/
for(int i =2;i<=n;i ++)
{
fibSum = fibNext+fibPre ;
fibPre = fibNext ;
fibNext = fibSum;
}
return fibSum ;
}

So the above implementation illustrates that the problem can be solved by using for loop instead of using recursion. The for loop is a constant running time with O(n), compared to what is an exponential growth in recursion
scenario.

Summary

Sometimes a problem seems to be a perfect fit for recursion can actually be solved by a simple for loop solution with better performance. When the result from the sub problem is not used efficiently by the recursion call stack and computation is done redundantly, the running time can grow explosively. This is when the recursion can go horribly wrong.

Find a cycle in a directed graph in Java

Recently I had to solve a problem that involving detecting cycle in a directed graph. I did some googling to see what other people have done. There are some good ideas on the web but nothing was exactly the right approach I’d like. So I wrote my own algorithm and Java implementation.

Directed Graph and DAG

In mathematics, a graph is a structure that consists of a group of nodes and the lines that connect these nodes. Each node is called a vertex and the lines that connect the nodes are called edges. A directed graph is a graph in which the edges have direction; they point from one vertex to another or from a vertex to itself. A real life example of a directed graph is a flow chart.

A directed graph can contain cycles. A cycle exists if we can, starting from a particular vertex, follow the edges in the forward direction and eventually loop back to that vertex. A graph that has no directed cycle is an directed acyclic graph (DAG).

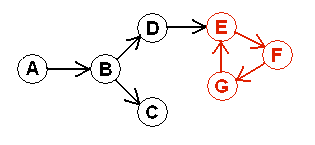
 Fig.1 A directed graph containing a cycle

When coding a directed graph you should consider different ways of implementing it depending on how connected your data is and what types of algorithms you’ll be using. We’ll show one way below, then we’ll implement a hasCycle() method which is based on a breadth-first topological sorting algorithm.

Implement Graph in Java

The implementation our graph will need a Graph class and two other classes, Vertex and Edge. We could have had only edges, each with a source and destination property, and let the vertices be implied but then we could not represent disconnected vertices. So let’s first look at how the Edge class is implemented.

public class Edge {

   public Vertex destination; // The destination Vertex of the Edge

   public Edge( Vertex d ){

      destination = d;

   }

}

Notice Edge stores a reference to the destination Vertex but not the source Vertex. That’s because in the Vertex class, we’ll store a list of the outbound Edges. This means that algorithms that need to traverse our graph can efficiently go from a Vertex to one of its outbound Edges, then to that Edge’s destination Vertex and so forth.

public class Vertex {

   public String name;

   public List<Edge> outEdges; // The out-bound Edges of this Vertex

   public int inDegree; // A convenient *scratch variable* for our algorithm to use

   public Vertex( String nm ){

      name = nm;

      outEdges = new LinkedList<Edge>();

      InDegree = 0;

   }

}

Now we can write an interface for our graph.

interface Graph {

   public Set<Vertex> vertices(); // Return all Vertices in the Graph

   public addVertex( String name );

   public void addEdge( String sourceName, String destName );

   public long size(); // Return the number of Vertices in the Graph

}

An implementation of Graph would store a collection of Vertices. The collection could be a Map with key of Vertex name for instance.

Implement the Search Method

Let’s look at an algorithm which will determine if our graph contains a cycle. There are different approaches to this problem – we’ll look at another way in a future post. In this method we use the idea that a directed graph whose vertices each have at least one incoming edge is itself a cycle. So our search will continue to remove vertices and their out-bound edges until what remains meets that condition. If we traverse the whole graph without seeing that condition then there is no cycle.

public static boolean hasCycle(DirectedGraph graph){

   if (graph == null || graph.size() == 0) return false;

   Collection <Vertex>vertexCollect = graph.vertices();

   Queue <Vertex> q; // Queue will store vertices that have in-degree of zero

   long counter = 0;

   /* Calculate the in-degree of all vertices and store on the Vertex */

   for (Vertex v: vertexCollect)

      v.inDegree = 0;

   for (Vertex v: vertexCollect){

      for(Edge edge : v.outEdges())

         edge.dest().inDegree++;

      }

   /* Find all vertices with in-degree == 0 and put in queue */

   q = new LinkedList<Vertex>();

   for (Vertex v : vertexCollect){

      if (v.inDegree == 0)

         q.offer(v);

   }

   if(q.size() == 0){

   return true; // Cycle found – all vertices have in-bound edges

   /* Traverse the queue counting Vertices visited */

   for (counter = 0; !q.isEmpty(); counter++) {

      Vertex v=q.poll();

      for (Edge e: v.outEdges()){

         Vertex w = e.dest();

         if(–w.inDegree == 0){

            q.offer(w);

         }

      }

   }

   if (counter != vertexCollect.size() ){

      return true;  //Cycle found

   }

   return false;

}

Summary

So we start by calculating the starting inDegree for each Vertex. Each Vertex with inDegree == 0 is put into a queue. These Vertices are starting points for processing. We begin the search from a Vertex in the queue, following the Edges and keeping a count of the Vertices visited. We decrement the inDegree of Vertices as their in-bound Edges are processed. Vertices whose inDegree goes to zero are put into the queue. When we reach the end of a branch where there are no more out-bound Edges, we take another Vertex from the queue and traverse. If we empty the queue before we’ve visited all the Vertices then we’ve found a cycle.

Our algorithm is essentially a modified topological sort. It is based on a breadth-first search (BFS) stategy – all sibling outEdges of a Vertex are processed before moving down to the next layer of Vertices. It has a linear running time of O (|V| + |E|). In the worst case scenario there would be no cycle in the graph and we’d visit each Vertex and each Edge.

There are other approaches. Instead of using a BFS, we could use DFS (depth-first search). A typical DFS would be written with a recursive method. To find a cycle, instead of tracking inDegree and number of vertices visited, it would be looking for the condition of visiting a vertex twice in the same branch.

In a future post, Floyd’s Algorithm – Tortoise and Hare, we explore an alternate approach to finding cycles.